[9] Declarando tipos e classes

Neste post vamos explorar os mecanismos utilizados para declarar novos tipos e classes em Haskell

Declarando tipos

A maneira mais simples de declarar um novo tipo é introduzir um sinônimo a um tipo existente. Veja a declaração abaixo, que define o tipo String como um sinônimo para o tipo [Char]:

type String = [Char]

Lembre-se que nomes de tipos devem iniciar com a letra maiúscula. Observe ainda que a declaração de tipos pode ser aninhada, isto é, podemos utilizar qualquer tipos existentes para definir um novo, inclusive tipos que nós mesmos tenhamos definido:

type Pos = (Int,Int)
type Trans = Pos -> Pos

No exemplo acima, estamos definindo um tipo Pos, que representa uma posição em um plano, e Trans uma função que transforma uma posição em outra. Um detalhe importante é que definições de tipo utilizando-se a construção type não pode ser recursiva, isto é, não é permitido definir tipos em termos de si mesmo. Por exemplo, a definição abaixo não é permitida em Haskell:

type Arvore = (Int,[Arvore])

Com esta definição nós gostaríamos de definir uma árvore como um valor inteiro e uma lista de sub-árvores. É uma definição simples e natural se você se lembrar um pouco do que aprendeu sobre estruturas de dados. Infelizmente não é possível declarar estruturas assim usando type, precisamos usar outro mecanismo, como veremos mais adiante.

Usando type conseguimos também definir tipos parametrisados. Por exemplo, se quisermos definir um novo tipo para representar um par de valores do mesmo tipo, podemos criar um sinônimo para isto, e usá-lo em uma função:

type Par a = (a,a)

somar :: Par Int -> Int
somar (a,b) = a + b

Declarações com mais de um parâmetro também são possíveis. Por exemplo, podemos declarar um tipo que representa uma associação entre chave e valor, e pode ser usado com uma tabela de valores. Veja abaixo também uma possível utilização desse novo tipo:

type Assoc k v = [(k,v)]

buscar :: (Eq a, Eq b) => a -> Assoc a b -> [b]
buscar k xs
    | xs == [] = []
    | k == fst (head xs) = snd (head xs) : buscar k (tail xs)
    | otherwise = buscar k (tail xs)

Declarando tipos usando data

A declaração de tipos totalmente novos, diferentemente do que fizemos com type, que declara sinônimos, pode ser feita usando a construção data. Por exemplo, é assim que o tipo Bool contido no Prelude, pode ser definido, composto por dois novos valores, True e False:

data Bool = False | True

Neste tipo de construção, o símbolo | é tipo apenas como um separador para os valores do tipo, chamados de construtores. Assim como nos tipos em si, os nomes dos construtores deve iniciar com letra maiúscula. Também precisamos ter o cuidado para não utilizamos o mesmo construtor em mais de um tipo.

Valores de novos tipos podem ser usados exatamente da mesma forma que tipos pré-existentes na linguagem, isto é, ser passados como parâmetros para funções, retornados como valores, etc. Por exemplo, podemos declarar o novo tipo abaixo, que representa de forma bastante básica os possíveis movimentos em um plano:

data Movimento = Norte | Sul | Leste | Oeste deriving Show

O trecho deriving Show é necessário apenas para o que GHCi consiga exibir os valores de Movimento na tela. Falaremos mais sobre isso mais adiante. Podemos criar as funções abaixo, capazes de manipular uma posição a partir de um ou uma série de movimentos:

mover :: Movimento -> Pos -> Pos
mover Norte (x,y) = (x,y+1)
mover Sul (x,y) = (x,y-1)
mover Leste (x,y) = (x+1,y)
mover Oeste (x,y) = (x-1,y)

movimentos :: [Movimento] -> Pos -> Pos
movimentos [] p = p
movimentos (m:ms) p = movimentos ms (mover m p)

rev :: Movimento -> Movimento
rev Norte = Sul
rev Sul = Norte
rev Leste = Oeste
rev Oeste = Leste

Os construtores definidos em uma declaração data também podem ter parâmetros. Por exemplo, imagine as declaração abaixo, que definem os valores possíveis para uma Forma:

data Forma = Circulo Float | Retangulo Float Float

Em outras palavras, o tipo Forma tem dois valores, Circulo r, onde r representa o raio do círculo, e Retangulo l a, onde l e a representam a largura e altura, respectivamente. Estes construtores podem ser usados para criar funções sobre formas, como produzir um quadrado a partir de um valor para o tamanho do lado, e para calcular a area de de uma forma:

quadrado :: Float -> Forma
quadrado n = Retangulo n n

area :: Forma -> Float
area (Circulo r) = pi * r ^ 2
area (Retangulo l a) = l * a

Declarações de tipos também podem ser parametrisadas. Por exemplo, o tipo Maybe, declarado no Prelude:

data Maybe a = Nothing | Just a

Esta declaração introduz o tipo Maybe a, cujo valor pode ser Nothing, ou da forma Just x, para um valor x do tipo a. Geralmente o tipo Maybe é usado pare representar funções que podem falhar, retornando Nothing quando ela de fato falhar, ou Just x com o resultado do processamento som sucesso. Por exemplo, poderíamos redefinir a função buscar introduzida a poucos instantes para utilizar o tipo Maybe:

type Assoc k v = [(k,v)]

buscar :: (Eq a, Eq b) => a -> Assoc a b -> Maybe b
buscar k xs
    | xs == [] = Nothing
    | k == fst (head xs) = Just (snd (head xs))
    | otherwise = buscar k (tail xs)

Nesta nova definição, a função buscar vai retornar a primeira ocorrência do valor associado à chave k. Caso o valor não exista na estrutura de dados, o valor Nothing é retornado.

Declarações newtype

Caso um novo tipo tenha um único construtor, com apenas um tipo, você pode usar a construção newtype. Por exemplo, podemos declarar um novo tipo para representar os números naturais, isto é, inteiros não negativos:

newtype Nat = N Int

Nesta construção, o construtor N recebe apenas um argumento do tipo Int, e é responsabilidade do programador garantir que o valor usado seja sempre não-negativo. Você pode estar se perguntando qual de fato é a diferença entre as três formas de declaração de tipos que vimos até agora. Primeiro como poderíamos declarar o tipo Nat usando as construções type e data:

type Nat = Int
data Nat = N Int

Bom, usando newtype em vez de type faz Haskell entender que Nat e Int são de fato diferentes, não permitindo que um tipo seja usado no lugar do outro, dando uma maior segurança ao programa através da checagem de tipos. Em comparação a data, usar newtype traz vantagens de desempenho, pois o compilador remove os construtures logo após a checagem de tipos, não adicionando nenhum custo computacional extra durante a avaliaçao. Em resumo, usar newtype sempre que possível no lugar de data vai dar mais segurança do ponto de vista de tipos sem prejudicar a performance.

Tipos recursivos

Novos tipos definidos através de data e newtype suportam a definição recursiva. Como exemplo, veja como podemos definir o tipo de números naturais, visto na seção anterior, através de uma definição recursiva:

data Nat = Zero | Suc Nat

Assim, Nat pode assumir os valores Zero ou um valor na forma Suc n, para algum valor do tipo Nat. Como pode ser percebido, esta definição permite a existência de uma sequencia infinita de números, começando com o valor Zero e continuando com a aplicação do construtor Suc ao valor anterior da sequencia:

Zero
Suc Zero
Suc (Suc Zero)
Suc (Suc (Suc Zero))
Suc (Suc (Suc (Suc Zero)))
Suc (Suc (Suc (Suc (Suc Zero))))
.
.
.

Desta forma, valores do tipo Nat correspondem aos números naturais com Zero representando o número 0, e Suc representando a função sucessor (1+). Por exemplo, Suc (Suc (Suc Zero) representa ` 1 + (1 + (1 + 0)) = 3`. Podemos então definir a seguintes funções de conversão entre naturais e inteiros:

nat2int :: Nat -> Int
nat2int Zero = 0
nat2int (Suc n) = 1 + nat2int n

int2nat :: Int -> Nat
int2nat 0 = Zero
int2nat n = Suc (int2nat (n-1))

De posse dessas funções, um número natural pode ser somado a outro convertendo-os primeiro para inteiro, operando a soma e depois convertendo o resultado para natural:

somar :: Nat -> Nat -> Nat
somar m n = int2nat (nat2int m + nat2int n)

Uma outra forma, mais eficiente, de definir a função soma, seria apenas adicionar a quantidade de construtores Suc à frente do segundo número de acordo com o primeiro:

somar :: Nat -> Nat -> Nat
somar Zero n = n
somar (Suc m) n = Suc (somar m n)

Árvores!

Agora que sabemos como definir tipos recursivamente, podemos definir uma árvore da forma correta na linguagem. Considere a árvore binária balanceada de busca abaixo para os demais exemplos nesta seção:

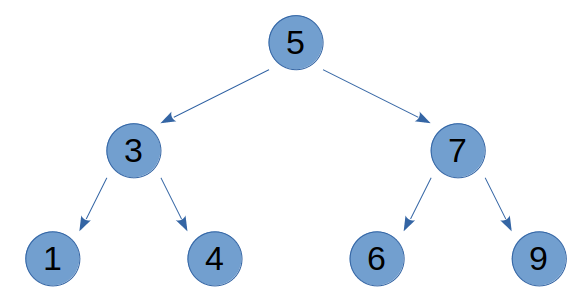
Neste exemplo, 1, 4, 6 e 9 são folhas, e os números 5, 3 e 7 são nós, ou vértices. Usando recursão, podemos definir um tipo para representar esta estrutura de dados:

data Arvore a = Folha a | No (Arvore a) a (Arvore a)

A árvore na imagem pode ser representada como:

t = No (No (Folha 1) 3 (Folha 4)) 5 (No (Folha 6) 7 (Folha 9))

Podemos considerar agora algumas funções em árvores:

existe :: Eq a => a -> Arvore a -> Bool
existe x (Folha y) = x == y
existe x (No esq y dir) = x == y || existe x esq || existe x dir

Traduzindo, um valor existe na folha se ele é igual ao valor naquela folha, e existe em um nó se ele é igual ao valor armazenado no nó ou existe na sub-árvore esquerda ou na sub-árvore direita. A função abaixo serializa uma árvore:

serializar :: Arvore a -> [a]
serializar (Folha x) = [x]
serializar (No e x d) = serializar e ++ [x] ++ serializar d

Aplicando esta função à árvore dada como exemplo teremos a lista [1,2,3,4,5,6,7,9]. Considerando a característica de árvores binárias de busca (a nossa árvore em particular é uma dessas), podemos melhorar um pouco a função existe:

existe :: Ord a => a -> Arvore a -> Bool
existe x (Folha y) = x == y
existe x (No esq y dir)
    | x == y    = True
    | x < y     = existe x esq
    | otherwise = existe x dir

Classes e declarações de instância

Vamos agora entender um pouco sobre classes. Em Haskell, uma nova classe pode ser definida utilizando-se a construção class. Por exemplo, a classe Eq pode ser definida da seguinte forma:

class Eq a where
    (==), (/=) :: a -> a -> Bool

    x /= y = not (a == y)

Observe que a definição da classe já introduziu uma definição para o operador /=, logo, a definição de uma instância pre cisa apenas da definição do operador ==. O tipo Bool pode se tornar um tipo Eq da seguinte forma:

instance Eq Bool where
    False == False = True
    True == True = True
    _ == _ = False

IMPORTANTE: apenas tipos definidos utilizando-se data e newtype podem ser instâncias de classes. Definições padrão, como o que acontece com o operador /= podem ser sobrescritos se for a vontade do programador.

Classes também podem ser estendidas para formar novas classes, como ocorre com a classe Ord, de tipos cujos valores são totalmente ordenáveis, é declarada no Prelude como uma extensão da classe Eq:

class Eq => Ord a where
    (<),(<=),(>),(>=) :: a -> a -> Bool
    min, max          :: a -> a -> a

    min x y | x <= y    = x
            | otherwise = y

    max x y | x <= y    = y
            | otherwise = x

Como a classe já inclui definições padrão para min e max, só é necessário definir os operadores de comparação:

instance Ord Bool where
    False < True = True
    _     < _    = False

    a <= b       = (a < b) || a == b
    a >  b       = b < a
    a >= b       = b <= a

Instâncias derivadas

Quando novos tipos são declarados é uma boa prática faze-los instâncias das classes padrão apropriadas. Haskell nos fornece uma construção que nos permite fazer nossos tipos instâncias das classes Eq, Ord, Show e Read, através da construção deriving. Por exemplo, o tipo Bool é definido desta forma no Prelude:

data Bool = False | True deriving (Eq, Ord, Show, Read)

Com isso, todas as operações definidas em Eq, Ord, Show e Read agora podem ser usadas com valores lógicos.